02 electro-optic modulator and electro-optic modulation optical frequency comb
Electro-optical effect refers to the effect that the refractive index of a material changes when an electric field is applied. There are two main kinds of electro-optical effect, one is the primary electro-optical effect, also known as the Pokels effect, which refers to the linear change of material refractive index with the applied electric field. The other is the secondary electro-optical effect, also known as the Kerr effect, in which the change in the refractive index of the material is proportional to the square of the electric field. Most electro-optical modulators are based on the Pokels effect. Using the electro-optic modulator, we can modulate the phase of the incident light, and on the basis of the phase modulation, through a certain conversion, we can also modulate the intensity or polarization of the light.
There are several different classical structures, as shown in Figure 2. (a), (b) and (c) are all single modulator structures with simple structure, but the line width of the generated optical frequency comb is limited by the electro-optical bandwidth. If an optical frequency comb with high repetition frequency is required, two or more modulators are required in cascade, as shown in Figure 2(d)(e). The last type of structure that generates an optical frequency comb is called an electro-optical resonator, which is the electro-optical modulator placed in the resonator, or the resonator itself can produce an electro-optical effect, as shown in Figure 3.
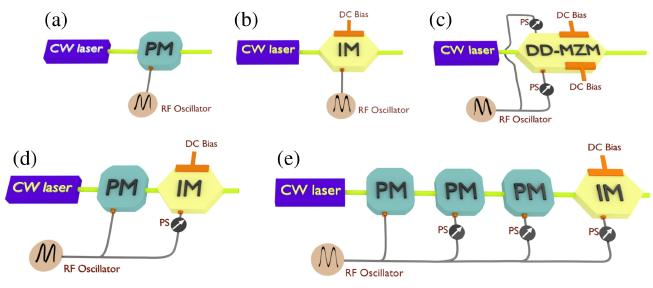
FIG. 2 Several experimental devices for generating optical frequency combs based on electro-optic modulators
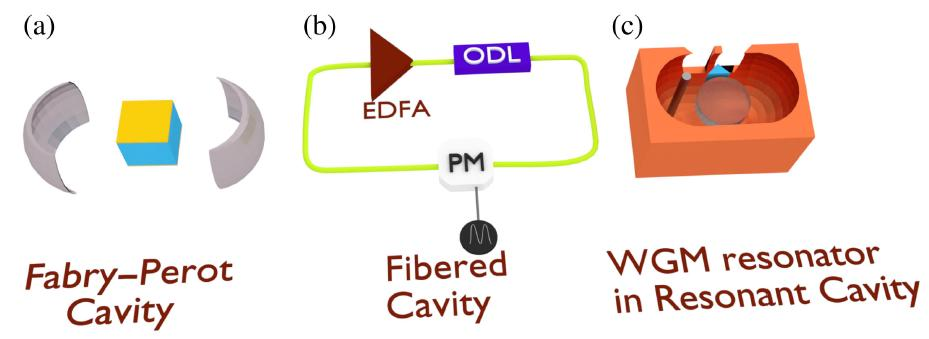
FIG. 3 Structures of several electro-optical cavities
03 Electro-optic modulation optical frequency comb characteristics
Advantage one: tunability
Since the light source is a tunable wide-spectrum laser, and the electro-optical modulator also has a certain operating frequency bandwidth, the electro-optical modulation optical frequency comb is also frequency tunable. In addition to the tunable frequency, since the waveform generation of the modulator is tunable, the repetition frequency of the resulting optical frequency comb is also tunable. This is an advantage that optical frequency combs produced by mode-locked lasers and micro-resonators do not have.
Advantage two: repetition frequency
The repetition rate is not only flexible, but also can be achieved without changing the experimental equipment. The line width of the electro-optic modulation optical frequency comb is roughly equivalent to the modulation bandwidth, the general commercial electro-optic modulator bandwidth is 40GHz, and the electro-optic modulation optical frequency comb repetition frequency can exceed the optical frequency comb bandwidth generated by all other methods except the micro resonator (which can reach 100GHz).
Advantage 3: spectral shaping
Compared with the optical comb produced by other ways, the optical disc shape of the electro-optic modulated optical comb is determined by a number of degrees of freedom, such as radio frequency signal, bias voltage, incident polarization, etc., which can be used to control the intensity of different combs to achieve the purpose of spectral shaping.
04 Application of electro-optic modulator optical frequency comb
In the practical application of electro-optic modulator optical frequency comb, it can be divided into single and double comb spectra. The line spacing of a single comb spectrum is very narrow, so high accuracy can be achieved. At the same time, compared with the optical frequency comb produced by mode-locked laser, the device of electro-optic modulator optical frequency comb is smaller and better tunable. The double comb spectrometer is produced by the interference of two coherent single combs with slightly different repetition frequencies, and the difference in repetition frequency is the line spacing of the new interference comb spectrum. Optical frequency comb technology can be used in optical imaging, ranging, thickness measurement, instrument calibration, arbitrary waveform spectrum shaping, radio frequency photonics, remote communication, optical stealth and so on.

FIG. 4 Application scenario of optical frequency comb: Taking the measurement of high-speed bullet profile as an example
Post time: Dec-19-2023





